因为疫情的原因，在家滞留了大半年，期间在家用一个半月的时间写完了硕士毕业论文，现在算是慢慢闲下来了，终于可以随便看看paper写写博客了。找了一篇最近预发表的CNN综述(2020年4月)，通篇读下来还是发现了一些基础知识上的盲区，比如分类问题上的loss除了有最常见的交叉熵，还有进一步考虑类内距离和类间距离的loss，主要用于人脸识别和ReID等领域。下面针对这方面的工作做一些归纳和记录。
问题概述
在回归问题上，ground truth是连续值，因此用L1距离或L2距离就能比较合理地度量预测值和ground truth之间的偏差。由此形成的优化空间也比较平滑，易于朝着正确的方向收敛。但是在分类问题上，ground truth是离散值，经过softmax处理后变成了one-hot编码，此时编码与编码之间的L1/L2距离是没有意义的，所以通常用交叉熵来度量预测值和ground truth这两个分布之间的近似程度。
交叉熵也被称为softmax loss，模型最后一层softmax的输入x经过$e^x$处理并归一化后，大的值会更大，小的值会更小，相当于强化了类与类之间的分离，形成大的类间距离，这是有助于进行分类的。
$L_{cross\;entropy}(x, class)=-log\;p_{class}=-log(\frac{e^{x[class]}}{\sum_j e^{x[j]}}\;)$
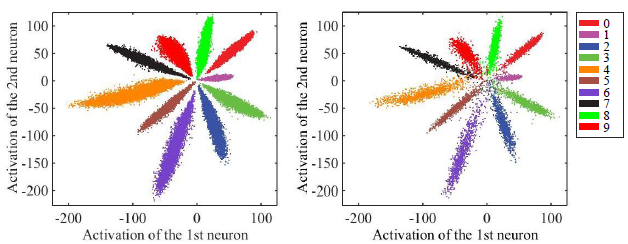
如下图，把用于MNIST手写体识别的卷积网络最后一层的feature维度设为2，由此可以在二维平面上显示所属不同类别的feature的空间分布情况。可以看到，不同类之间有着明显的间隔，非常易于分类。但另一方面，虽然类间距离大了，但类内距离也很大，每一类的低维流形（manifold）有着较大的方差，通俗的来说就是散点分布比较广泛，不紧凑。这对于普通的ImageNet分类这种问题影响不大，但对于人脸识别这种需要identification和verification的任务来说，具有很大的影响。
具体的来说，人脸识别（identification）是要把一张输入的人脸图抽出来的feature分成不同的身份（identity），即分成不同的类，底库中有多少个ID，就有着多少个类。它要求类与类之间的距离尽可能地远，即类间距离（inter-personal variations）大，间隔越大越清晰，才能分得越准确，减小误识率（false accept rate）。而人脸验证（verification）则是要判断来自同一个人的两张人脸feature，是否会被正确分类成同一个ID，是一个二分类问题。它要求属于同一类的feature尽可能地靠得近，即类内距离（intra-personal variations）小，分布地紧凑（compactness），才能提高准确率（true positive rate）。
如下图，是MegaFace数据集中的样本，左边是属于同一个人A的不同照片，右边是不同人（A、B、C、D等）的照片。identification的过程是在训练时把ABCD等的人脸图通过CNN提取feature，映射成低维空间上的对应向量；verification的过程是在测试时把A的人脸图的feature，同底库中A的人脸feature做对比，看是否靠得足够近以判断它们是属于同一个人。如果采用了普通的softmax loss，类间距离虽然有较为清晰的界限，易于identification，但类内距离较大，不易于verification。
下图是一些典型的出错场景。False accept，本来不是同一个人，错误地被判断成是同一个人，说明它们各自的feature没有分得足够开；False reject，本来是同一个人，错误地被判断成不是同一个人，说明这个人的多个feature不够紧凑。
下面以人脸识别为任务场景，介绍常用的改善类间距离和类内距离的几种经典loss。
Contrastive loss（DeepID 2/DeepID 2+/DeepID 3）
主要思想
该loss最早是由2006年的一篇CVPR以降维方法的形式所提出[1]，随后在2014年被商汤的DeepID 2[2]、DeepID 2+[3]、DeepID 3[4]系列使用在深度学习人脸识别领域上。中心思想就是拉近同类点的距离，推远非同类点的距离。麻烦一点的是，需要人为挑选出同类和非同类的图像对（O($n^2$)），来提供先验信息。
具体形式
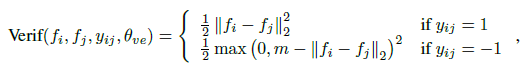上式中，$f$代表从人脸图提取出的特征矢量，当它们来自同一个人时（$y_{ij}=1$），取两个特征的L2距离作为loss值，意味着该距离在优化时会越来越小；当它们来自不同的两个人时（$y_{ij}=-1$），同样是取两个特征的L2距离，但是前面加了负号，意味着优化时该距离越大越好。同时，针对非同类距离还做了阈值m的截断处理，也就是说当距离远到大过m时，就忽略该项，这样做相当于只考虑周边临近点的影响，而不是盲目地排斥所有的非同类点，鲁棒性会更强，计算量也更小。
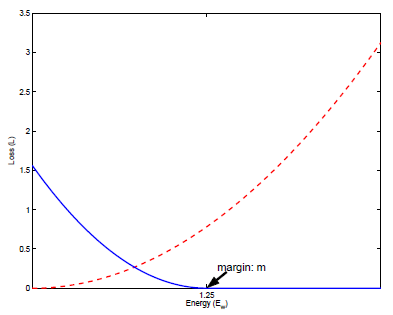
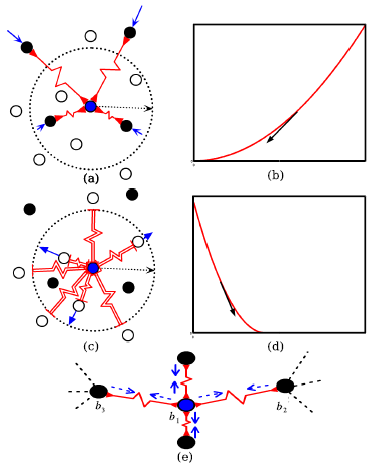
下图是该loss的曲线图，红色曲线代表同类点间的loss，蓝色曲线代表非同类点的。作者将其类比成弹簧-振子系统，具有很直观的物理意义，很符合直觉。
实验过程
想想如果只用contrastive loss会怎样？同类点会不断地相互抱团吸引，领域内的非同类点相互排斥，最终会使得同类点形成方差极小的团簇。但是，这里忽略了一个重要的点，就是不同类的团簇之间没有做距离限制，没有明显的分类界限，团簇与团簇之间可能挨得很近，甚至互相有重叠。这种情况下，verification会做得很好，但是identification就没法做了。
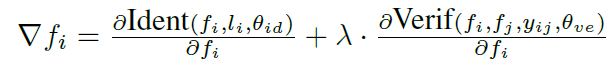在DeepID 2中，为了兼顾这两种任务，将适合加大类间距离的softmax loss，与适合减小类内距离的contrastive loss相结合，取权重$\lambda$来做平衡，并分别命名为identification和verification loss。下图是不同$\lambda$下，网络所提取的六个ID的高维特征示意图，为了清晰起见只用了前两个主分量来画图。
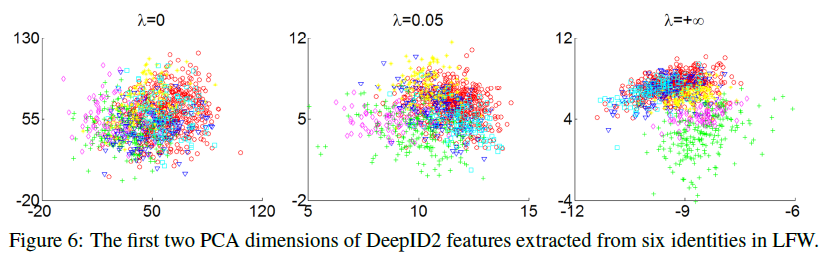可以看到，$\lambda=0$时只用了softmax loss，不同类的团簇之间易于区分，但同类的团簇过于分散；$\lambda=\infty$时只用了contrastive loss，同类团簇很集中，但不同类团簇之间重叠区域较大，不易于区分；$\lambda=0.05$时达到了较好的折衷，有较大的类间距离和较小的类内距离，此时的人脸识别任务能有较好的效果。
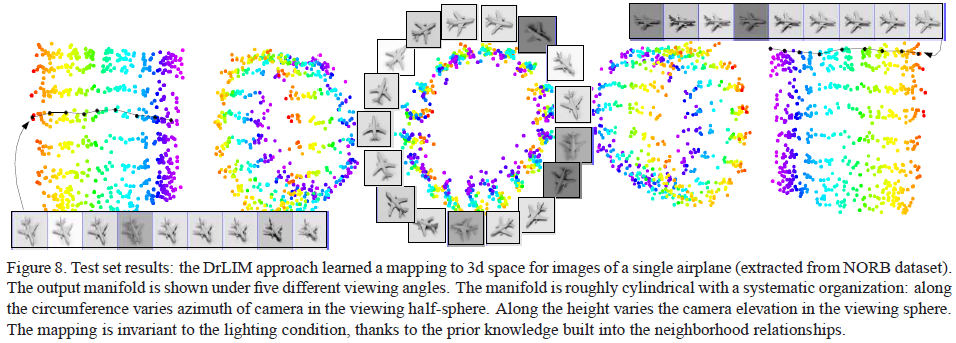
最后，展示一下contrastive loss原文[1]里一个非常精美的图。这里将其作为一个降维方法，它能够把不同亮度、不同角度下的同一架飞机的图片，均匀地映射成低维3d空间上的流形，且连续位置点上的特征对应着连续变化角度的输入。
相关的文献资料：
1. Contrastive loss原文: Dimensionality Reduction by Learning an Invariant Mapping
2. DeepID 2: Deep Learning Face Representation by Joint
Identification-Verification
3. DeepID 2+: Deeply learned face representations are sparse, selective, and robust
4. DeepID 3: DeepID3: Face Recognition with Very Deep Neural Networks
Triplet loss (FaceNet)
主要思想
前面的Contrastive loss在优化时针对类内距离和类间距离是分开处理的，二者之间没有关联，各优化各的。接下来要介绍的Triplet loss，把类内和类间距离协同考虑，不要求它们各自达到最小和最大，只要求类内距离小于类间距离就可以，为安全起见，二者之间还设了一个余量空间（margin）。直观地感受，优化标准变得更加普适和明确了。同时，在Contrastive loss中，有O($n^2$)个图像对的loss需要backward，但是在这里，只需要在同类中找出距离最大的、在非同类中找出距离最小的来计算loss，一个batch中只需要一次backward就可以。
具体形式
对于一张任意的候选人脸$x_i^a$，所有与之同类的人脸$x_i^p$（positive），以及所有与之非同类的人脸$x_i^n$（negative），需要满足类内距离加余量$\alpha$小于类间距离，即有以下的目标关系：
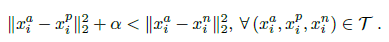上式经过移项调整，就可得统一的loss形式：
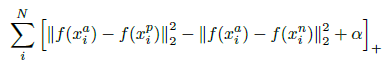但在实际优化过程中，如果像contrastive loss那样遍历所有的图像对来计算上述loss，图像对中有大量的easy case，不等式条件很容易就会被满足，从而导致收敛缓慢。所以需要人为挑选不满足条件的hard case，才能推动优化朝着正确的方向前进。针对$x_i^a$，需要在同类样本中找到hard positive $x_i^p$使得有最大的类内距离；需要在非同类样本中找到hard negative $x_i^n$使得有最小的类间距离：
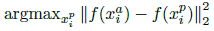
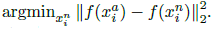
实验过程
在上一节中提到，需要找到两个极值的类距离，如果对象是整个训练集，计算一个样本$x_i^a$与其它所有样本的距离需要O(n)次，排序还需要O(nlogn)次操作，不预先储存的话还需要在所有n个样本上重复上述操作，实际是不可行的。同时还可能会受到误标的噪声数据影响。
在FaceNet[5]中，提出了两种解决方法。一种是离线计算并储存法，每迭代n步计算一次类距离的极值，而且还只是在训练集的子集上。另一种是在线mini-batch计算法，在大小约为1800的batch上计算类距离极值，计算量得以简化。
另外文中还发现，在训练初期，只计算同类样本的距离会使得收敛更稳定。在训练中后期，才慢慢加入非同类样本，而且为了防止陷入局部次优点，加入的不是hardest negative样本（考虑到会受误标数据的影响），而是semi-hard negative样本$x_i^n$，这部分样本可能处在余量空间内，但依然能有效促进优化的进行。
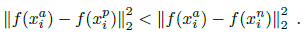下图是不同pose不同光照下的效果图，每一行左右两张图来自同一个人，数字代表两两之间的特征距离。当阈值设为1.1时，人脸识别的结果就是正确的，表明当前的模型对pose和光照的鲁棒性还是较强的。
5. FaceNet: FaceNet: A Unified Embedding for Face Recognition and Clustering
Center loss
主要思想
前面介绍的两种loss，是基于两个和三个“图像对”指示出优化的梯度方向，虽然合理地避免了在庞大数据集上计算梯度，但是需要计算的图像对的数目很大，同时优化过程也不是很稳定和高效，计算复杂度比较高。ECCV 2016提出的center loss[6]，没有采用图像对的策略，而是定义出每一类特征的中心点，根据每一类样本与对应中心点之间的距离作为类内距离来优化，与contrastive loss的优化目标很相似，只不过不再需要人为提取同类和不同类的图像对，优化过程和普通SGD中的普通loss没什么区别，减小了计算复杂度。
具体形式
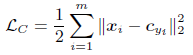上式中，m代表batch样本数目，$c_{yi}$即代表第i类特征的中心点。在初始化时，它由网络所提取的第i类特征矢量取平均得来，在随后的迭代过程中，由于网络的权重参数不断地在更新，每一类的特征矢量也在逐渐变化，为了不浪费之前迭代步中所计算出的中心点，并没有重新取平均求中心点，而是对中心点以梯度下降的方式更新：
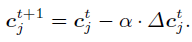其中，梯度是根据损失值$L_c$对中心点$c_{yi}$求导得来：
$\Delta c_j = \frac{\partial L_c}{\partial c_{yj}} = \sum_{i=1}^m (c_{yj}-x_i)$
同contrastive loss一样，center loss只关注了减小类内距离，因此还需要softmax loss来辅助做类间分离，二者之间用$\lambda$系数作平衡。最终总loss如下：
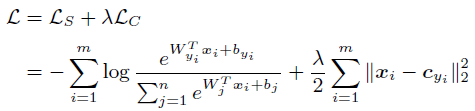
实验过程
计算类的中心点时，如果对象是整个训练集，计算量会很大。因此在原文中，采取了与triplet loss相同的mini-batch策略，只在一个batch的样本集上取平均，往后的每次迭代都用梯度更新的方式来不断修正中心点的位置。
为了平衡softmax loss和center loss，原文中同样也进行了权重的调整，不同$\lambda$下的特征分布如下图，可见起到的作用与contrastive loss的相同。
6. Center loss原文: A Discriminative Feature Learning Approach for Deep Face Recognition
Large-Margin Softmax loss
主要思想
从名字就可以看出，该loss是softmax loss的加强版。在前面，我们介绍过softmax loss是通过softmax function刻意推远了类间距离，但这种推远也只是使类与类之间产生间隔，并没有像triplet loss那样留有优化空间上的余量。large-margin softmax loss沿用softmax loss的形式，但拓展到了更一般的形式，不仅要使类与类之间产生间隔，还要求这种间隔能成倍地扩大，形成巨大的类间“鸿沟”。这样一方面使得类间距离增大，另一方面相比较之下类内距离自然而然地就显小了。同时，由于刻意要求巨大的类间距离，优化目标变得很困难，使得过拟合的风险降低。
具体形式
普通的softmax loss形式如下：
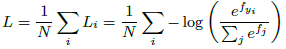视网络最后的全连接层为线性分类器，其参数为$W$，则特征$f$可展开为矢量相乘形式：
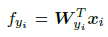把矢量点积按照向量模和夹角相乘的形式展开：
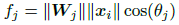那么softmax loss可重新写为
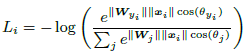为了在不同类之间产生间隔，需要使得
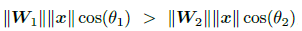问题的关键来了，想要更严格地控制类间距离，可针对上式做一个缩放，在余弦角上施加正整数因子m，m越大，缩放地更严重，不等式条件更严格，类间距离就越大。
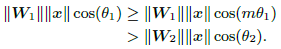因此，large-margin softmax loss的公式为
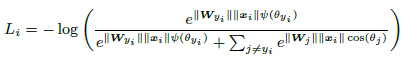其中，
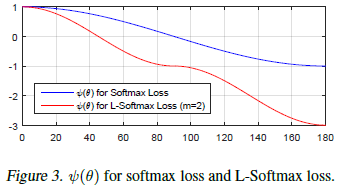
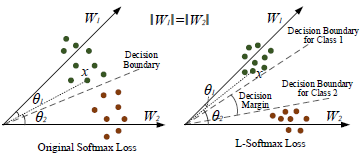
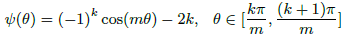上式中，k是[0, m-1]之间的整数。两种loss的曲线对比如下图，可以看到softmax loss是m=1时的特例，当m大于1时，限制条件要更加严格。从特征分布示意图也可以看出，large-margin softmax loss的类间距离要更大。
实验过程
在原文[7]的实验中， 作者认为L-Softmax loss的收敛难度太高，因此在训练的初期，为了加速收敛，采用原始的softmax loss作为起点，在后期逐渐地过渡到m大于1的L-Softmax loss上。
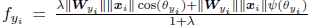上式中，训练初期$\lambda$很大，相当于softmax loss，随后慢慢减小到接近于0（但不会是0）的小数，此时才成为L-Softmax loss。在不同的缩放因子m下，MNIST手写体的特征分布图如下：
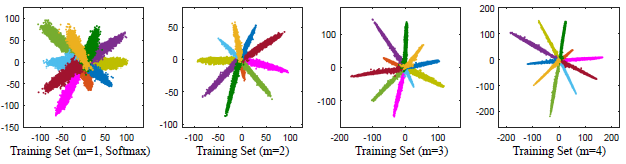可以看到，类间距离确实增大了，但感觉类内距离还是很大，同类流形的方差大，不紧凑。虽然原文中声称the minimum inter-class distance being greater than the maximum intra-class distance.，但我个人感觉这点效果还是没有达到的。
7. L-Softmax loss原文: Large-Margin Softmax Loss for Convolutional Neural Networks