在detection任务中，需要对候选框的坐标位置进行回归。常用的loss有L1、Smooth L1、L2，但它们的参数都是未归一化的，容易受框的尺寸影响，后来又有IoU这种归一化过的尺寸无关loss，但它也有优化缓慢、未重叠框无法优化等缺点，于是又有人在IoU的基础上进行各种改进，本文将会介绍这些改进版的IoU loss。
L1/L2 loss
对框最直接的表达，就是描述其中心点坐标以及长宽，$\lbrace x_{center},y_{center},w,h \rbrace$，或者是四个点的坐标，$\lbrace x_{top-left},y_{top-left},x_{bottom-right},y_{bottom-right}\rbrace$。对于anchor-based方法，可以用坐标的偏移量offset来回归，即学习其残差，如$\lbrace x_{center-offset},y_{center-offset},w_{offset},h_{offset} \rbrace$，$\lbrace x_{top-left-offset},y_{top-left-offset},x_{bottom-right-offset},y_{bottom-right-offset}\rbrace$。
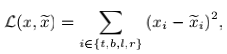直接用L1/L2距离对它们进行回归，思路很直接，但是这种方式存在两个缺点：一，它把一个整体的框看成四个独立的点，优化过程中没有考虑整体性，容易出现某一两个点离真实点很近，但另外两个点却离真实点偏离很远，此时依然有较小的loss；二，它的参数都没有归一化，这样“在大框上小的误差”和“小框上大的误差”会被等同看待，但其实后者对整体精度的影响要大得多，由此小框上的localization会很差。
IoU loss
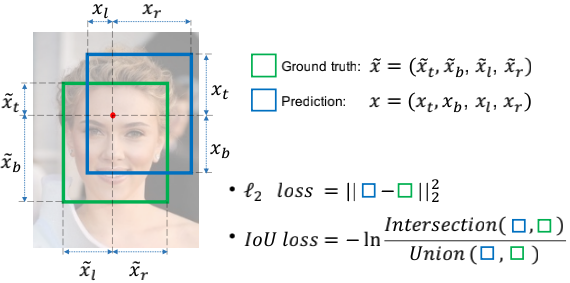为了解决L1/L2 loss的上述缺点，IoU loss被提出，它的思路很简单，直接面向目标优化，追求预测框与真实框的最大重合。框被当成一个整体看待，同时分数也是一个无量纲的比值，也就避免了之前的缺点。
但它也不是完美的，设想一下极端的情况，假如一开始预测框与真实框就离得太远，没有重叠部分，那该怎么优化？此时一开始loss就是0，且无法指示优化的方向，完全无法优化下去。当然这只是理论上会发生，实际上候选框会经过手动排序和选择，尽量避免这种情况的发生。
GIoU loss（CVPR 2019）
为了专门解决IoU loss在框未重叠时的优化问题，引入了泛化的Generalized IoU（GIoU）。设想有框A和B，先找出一个能同时覆盖A和B的最小凸多边形C，随后定义：
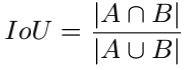
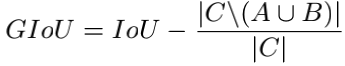关键就在于上式中的最后一项，分子代表C中排除掉A和B还剩下的区域。考虑两种极端情况，当A和B没有交集时，$IoU=0$，$GIoU=-\frac{C-A\cup B}{C}$，下限$GIoU=-1$不为0，依然能指示优化的方向，此时GIoU能减少C中除A和B之外的区域大小，迫使A和B整体相互靠近，达到相互重叠的目的；当A和B完全重合时(此时A=B=C)，$IoU=1$，上限$GIoU=1$，GIoU已经退化成了IoU。
具体到细节，如何找到A和B的最小凸多边形C？看起来挺麻烦，但好在在detection任务中，候选框都是矩形的，A和B都是矩形，那么C有理由也是矩形，只需要计算出同时覆盖住A和B的矩形即可。类似于计算交集的过程，只不过求min和求max反了过来：
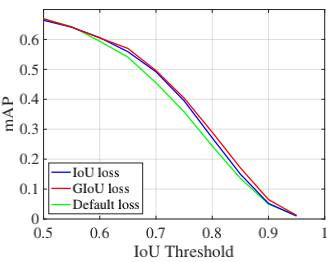
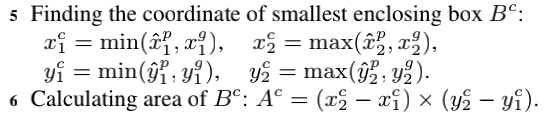直观地看一眼GIoU在Faster R-CNN上的结果，效果比IoU loss和L1-smooth loss都要好，尤其在高阈值区间这种差距更明显，说明使用GIoU会使得localization更准。
原文地址：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
DIoU loss（AAAI 2020）
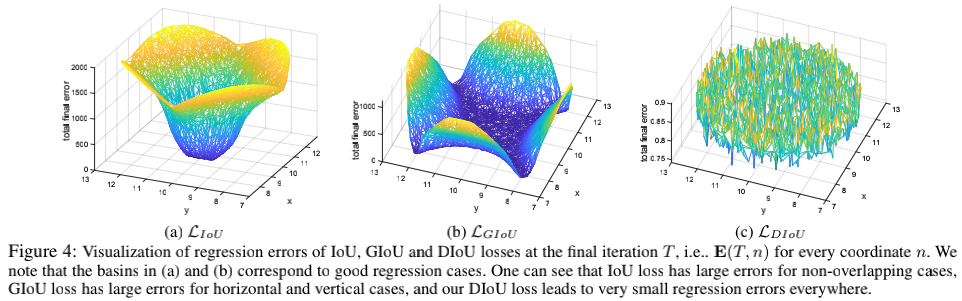
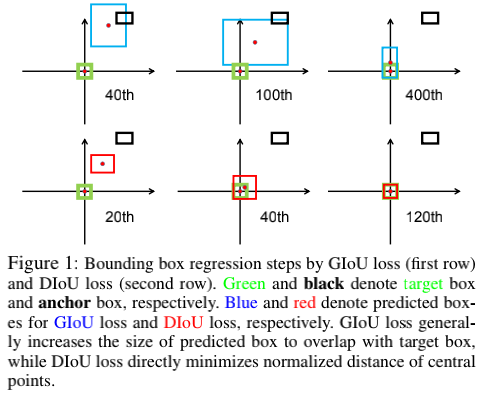GIoU有缺点吗？有。当A和B不重叠时，它的确能解决继续优化的问题，但这个过程太慢了，需要先迫使AB相交，再转化为IoU优化，这需要较多的迭代次数（如上图）；另一方面，当框很狭长时，GIoU的补偿项$\frac{C-A\cup B}{C}$很小，此时已经退化成IoU了，而GIoU和IoU对狭长框的回归效果都不好（如下图）。
为了解决这两个问题，提出了Distance-IoU（DIoU）Loss，它抛弃了GIoU中最小覆盖域C的使用，直接把IoU loss和L2 loss结合起来，既具有IoU loss整体性和尺寸无关性的优点，又有AB不相交时可继续优化的特点。虽然引入了L2距离，但经过了归一化，也变得跟尺寸无关。
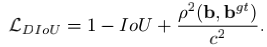
式中，最后一项以预测框和真实框的中心点距离为参考，并除以二者的对角距离，限定范围0-1。由于这一项的存在，框坐标回归的过程中是非常快的，即便是AB不相交，以及狭长框等hard case。
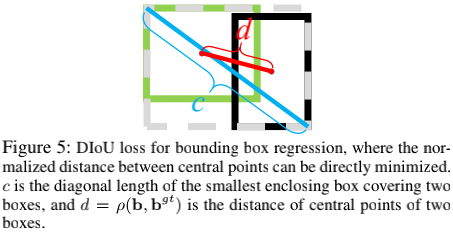
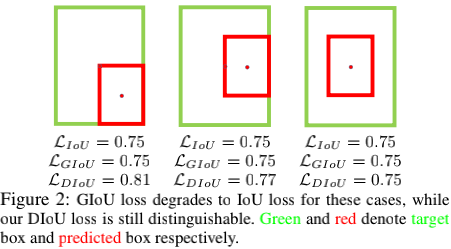DIoU的另一个优点，在于即使A完全覆盖B时，也不至于退化成IoU（此时GIoU已退化成IoU），依然能凭借L2距离项继续指示优化的方向（如上图）。基于这个特性，可以用DIoU代替传统的IoU来做框的非极大值抑制，能够更多地保留住有用的框（如下图），这被称为DIoU-NMS。
原文地址：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
CIoU loss（AAAI 2020）
CIoU其实和DIoU出自同一篇文章，这里为了清晰起见，把二者分开讲解。DIoU解决了IoU类loss训练缓慢的问题，但在精度上没有大幅度的提升。能否继续改进，让框的回归更快，同时更准？CIoU的目标便是如此。
文中总结了框回归的三要素：重叠区域大小、中心点距离、长宽比。IoU/GIoU loss只考虑了第一点，L1/L2 loss只考虑了第二点，DIoU loss同时考虑了第一和第二点。如果设计一种loss把上述三点考虑全了，应该就能达到又快又准的效果，这便是Complete IoU（CIoU）loss的思想。
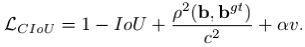CIoU形式如上，其实就是在DIoU的基础上，加了一项$\upsilon$，该项考虑的是长宽比，形式如下：
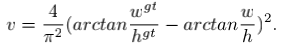然而，三要素之间存在优先级，第一点（重叠面积）要比第三点（长宽比）重要，尤其是在初始阶段AB尚未相交时，此时追求长宽比并没有那么重要，因此需要适当降低它的权重。所以长宽比项带了系数$\alpha$，它参考IoU的大小做了一次缩放：
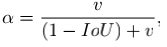在效果上，文中把上述所有的IoU loss都做了对比实验，结果如下。DIoU和CIoU对性能都有较明显的提升，CIoU配合DIoU-NMS的效果则更好。至于说为什么没有DIoU配合DIoU-NMS的组合，可能是因为效果不好？原因不明。另外，也没有CIoU-NMS这个东西，可能因为在挑选框的时候，长宽比根本不重要，只要重叠面积和中心距离足够近，这样的框就已经足够好了，但是作者是不是也做一下对比实验比较好？可能最终效果不好所以没放上来。
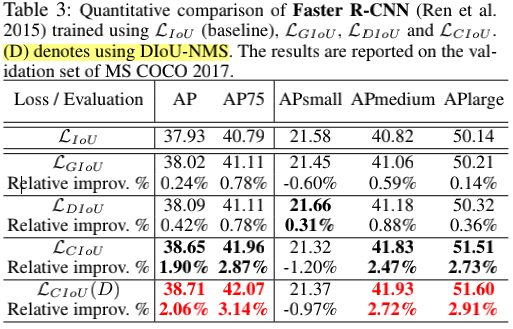上图中结果唯一反常的是，CIoU在小目标上的精度反而变差了，这也可以理解。因为小目标根本就不在乎长宽比了，在乎的是框的重叠和中心点的距离，此时过多地考虑了长宽比，反而会弱化另两个因素的影响。
原文地址：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression