针对mage classification, semantic segmentation等任务, 需要感受域越大越好, 这样在high-level的feature上看到的原始输入像素范围更大, 更有利于做出全局判断. 在detection等任务上, 为了检测到不同尺度大小的物体, 需要在不同感受域大小的feature上分别做检测. 但是, 感受域究竟需要大到多少? 真的是越大越有效吗? 针对这些问题调研了相关文献, 做了以下整理和记录.
感受域的计算
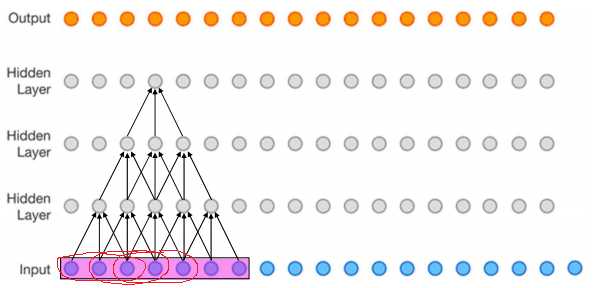
这里做自下而上的推导, 即从感受域为1的第一层卷积开始算起. 假设有如下三层kernel=(3, 3), stride=(1, 1)的Conv:
$r_{n}$ = 第n层的感受域
= 总的感受域(每个卷积点的感受域之和) — 重叠部分的感受域(相邻卷积点的感受域的重叠部分)
= 卷积核宽度 X 上一层的感受域 — (卷积核宽度 — 1) X (上一层的感受域 — 连续积累的stride)
= $k_n \times r_{n-1} - (k_n -1) \times (r_{n-1}-\prod_{i=1}^{n-1}s_i)$
= $r_{n-1} + (k_n-1)\times \prod_{i=1}^{n-1}s_i$
举例如下,
$r_1 = 1$
$r_2 = 1 + (3-1)\times 1 = 3$
$r_3 = 3 + (3-1)\times(1\times 1) = 5$
$r_4 = 5 + (3-1)\times(1\times 1\times 1) = 7$, 即上图中红色部分.
特殊地, 针对空间卷积dilation = r, 相当于拥有更大的卷积核$k^\prime = 1 + r(k-1)$. 针对池化pooling, 其kernel和stride等同于Conv来计算.
从公式中可以看到, 任何一层的stride是会被积累下来的, 对以后所有的层都会产生影响. 任何一层的kernel只在当前层显式地影响感受域. 所以要想迅速地增大感受域, 连续使用大于1的stride即可做到, 但那会急剧缩小feature map size. 使用大的kernel也可, 但大的卷积核会造成很大的计算量, 例如7x7Conv计算量很大, 但替换成两层连续的3x3Conv也能得到相同的感受域, 还能减少计算量, 再或者使用孙剑老师那篇"Large kernel matters"中提出的"1xk + kx1" Conv也可.
感受域真的越大越好吗? 这里出于好奇, 手动计算了一下ResNet-34的感受域, 在224x224大小的输入上, 最后一层Conv的感受域居然达到了900x900, 也就是说感受域已经溢出了输入图片的大小范围, 更不用说后面更深的ResNet-50, ResNet-101, ResNet-152. 既然感受域已经饱和, 那它们的预测能力也应该饱和才对. 但真实情况是如此吗? 不是, 网络依然是越深越好, 感受域越大越好. 所以这里引出了一个有效感受域的概念.
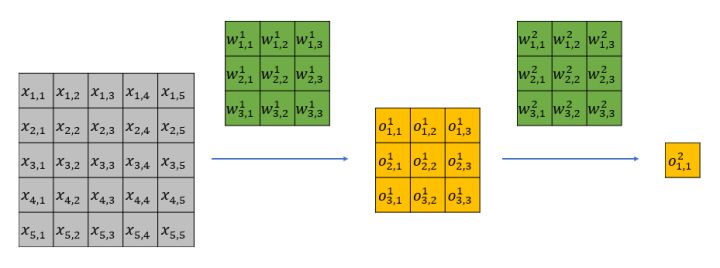
虽然感受域内所有的像素点都对最终结果有影响, 但是它们的权重不一样, 处于中心位置的点权重最大, 处于边缘位置的点权重最小. 例如, 图中边缘处的的$x_{1,1}$只能通过$o_{1,1}^1$来影响最终的$o_{1,1}^2$, 而中心处的$x_{3,3}$可以通过所有的$o_{1,1}^1, o_{1,2}^1, …, o_{3,3}^1$来影响最终的$o_{1,1}^2$. 直观地想象, 权重应该是从图片的中心点向边缘逐渐降低的. NIPS上有文章专门针对有效感受域做了分析, 证明权重是呈高斯型分布的, 这也与直觉相符, 下面就来看看这篇文章.
Understanding the Effective Receptive Field in Deep Convolutional Neural Networks (NIPS 2016)
理论推导
首先从最理想的情况开始, 令Loss在最后一层中心点上的梯度为1, 即$\frac{\partial Loss}{\partial y_{(0, 0)}}=1$, 其余非中心点的$\frac{\partial Loss}{\partial y_{(i, j)}}=0$, 这样可以只考虑对中心点的影响. 同时假设Conv层的kernel size = 1, 所有的权重都为1. 这样就有如下形式的梯度信号$u(t)$和卷积核信号$v(t)$ (t是像素点的下标):
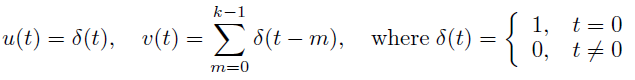在n层的卷积网络中, 逐层反向传播到第一层(也就是输入)上的信号就是$o=n\cdot v\cdot v\cdot…\cdot v$(一共n个$v$), 对其变换到频率域然后再变换回空间域, 得到:
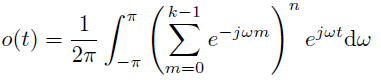上式的系数$e^{j\omega t}$展开后就是一个关于$t$的二项式, 具有高斯型的分布.
随后将这种特殊情况拓展到了一般情况(如卷积核权重是随机分布或高斯分布), 最终的结果也不会相差太远, 得到的都是一个高斯型分布的信号. 高斯分布意味着边缘点所占的权重非常小, 中心区域的点比重最大, 这些区域的点才是有效感受域(ERF). 最终大一统定性的结论有:
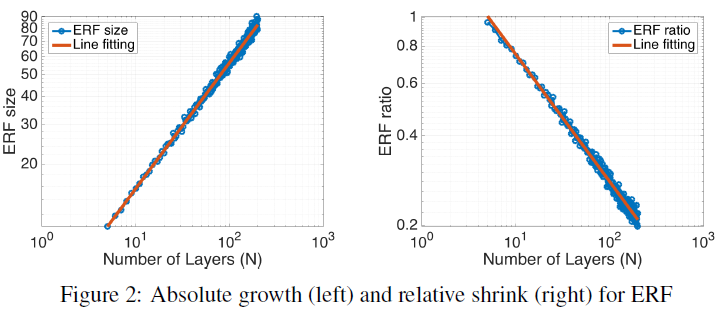
随着层数n的增加, 绝对ERF的增长速率是O($\sqrt n$), 相对ERF(ERF占RF之比)的增长速率是O($1/\sqrt n$): 通俗地解释, 随着层数的增加, ERF确实会增加, 但是不是像RF那样呈线性地增加, 而是呈开次方型的增加, 增长的加速度会逐渐放缓. 另一方面, ERF占RF的比例也在逐渐缩减, 即越靠后的层虽然RF越大, 但其中ERF的比例会越小. 这也就能解释前面ResNet-34最后一层的感受域虽然有900x900, 但其中ERF可能只占了比较小一部分, 所以继续增加层数能够继续增加ERF, 进而增加分类精度.
下采样和空洞卷积可以增加ERF, skip connection会减小ERF, drop out不改变ERF: 下采样(stride>1的Conv或pooling)会增加连乘累计的strides, 空洞卷积可以增加kernel size, 依据上一节计算感受域的公式, 这些都能使RF增加, 从而使ERF增加.
网络在经过训练后, ERF会自动增加: 经过训练, 网络自主学习到了要加强边缘像素点的联系, 所以自动调整边缘点的权重使得其重要性增加, 也就是ERF增加了. 同时, 文中提到, 在训练前后, 即使RF已经超过了原始输入图片大小, ERF依然未能超过原始图片大小. 说明要想让ERF真的覆盖整个输入图片, RF需要远远大于输入图片才行 ,这个时候就需要不断地堆Conv了.
改进措施
作者依据前面的分析, 提出了增大ERF的几点建议:
一, 在权重初始化时, 给中心点以较低的权重, 给边缘点以较高的权重. 这样在一开始时网络就能看到更大的范围, 虽然在训练过程中, 网络会自主调节权重, 但在一开始就让网络看到更全的东西, 是有益处的. 不过, 作者随后补充道, 这种方法带来的益处有限.
二, 使用更多五花八门的空洞卷积.
评价与思考
文中最后从人的视觉神经连接的角度去分析比较, 发现现有的卷积网络与视觉神经连接的特征相悖. 假设一下, 当层数n趋于无穷大时, RF变得无穷大, 而ERF在RF中占的比例是无穷小. 换成人眼看世界的方式, 当人在看一幅巨大的远景图时, 人眼变得只会关注其中某一个很小的点, 这显然与现实实悖, 现实中人眼会更加去感受全局的画面, 也就是说ERF会变得很大. 说明卷积网络与人的神经连接还是存在本质上的区别, 也就是说模仿得不到位.
该文从理论角度分析了有效感受域的范围, 虽然没有提出从本质上改善有效感受域的方法, 但是也给我们的工作带来了启示意义. 总的来说, 就是贪心地让感受域越大越好, 采用越大的卷积核甚至是空洞卷积核越好.
论文链接: Understanding the Effective Receptive Field in Deep Convolutional Neural Networks