Image inpainting using CFD methods

发表于 | 分类于
| 字数统计： 2616 | 阅读时长约 8 mins

  无意间翻阅了OpenCV计算摄影学篇章的教程, 主要有三部分: Image denoising, Image inpainting和HDR, 基本上对应着组里ISP方向现有的研究内容. 其中, 提到了一种使用计算流体动力学(Computational Fluid Dynamics/CFD)的方法来解决inpainting问题, 而CFD恰巧是我所熟悉的, 所以就找了对应的文献简单复现了一下, 下面做一些记录. 需要注意的是, 这里所涉及的都是传统算法, 与深度学习方法无关.

  • Image Inpainting (year 2000, cite 4088)

  这篇基本是inpainting方向最早的一篇有影响力的文章了. 在图像补全(inpainting)任务上, 需要参考邻域的像素值来对残缺区域做补全, 同时还要做到边缘过渡自然, 让人眼看不出这块是明显后来补上的. 就好像补衣服一样, 破掉的那块需要用跟衣服整体风格相似的步来补, 同时边缘的布线颜色以及走向需要和衣服的纹理相似, 这样才能补完浑然天成. 在photoshop上, 人工补全图片的过程大概是这样的, 把目标区域临近的像素块抠出来, 然后复制并平移到目标区域, 再对边缘处做过渡处理, 例如羽化和涂抹等操作. 在这里, idea就出来了, 既然是像素的平移, 能不能用更科学, 更soft的方法呢? 有, 让像素像流体一样流动. 这篇文章讲的就是这么一件事, 用CFD的方法让mask周围区域的像素像流体一样光滑地流动到mask区域.
  再直观地想一想细节, 流体在扩散过程中, 是沿着梯度最大的方向运动的, 这是符合物理的. 但如果在inpainting任务上, 图片中有纹理有不同颜色的像素块, 如果像素按照梯度最大的方向运动, 这些纹理都会被抹平, 所以为了保留纹理信息, 这里与CFD不同的是, 需要让像素按照梯度的法向方向去运动.

理论推导

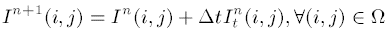
  文中用$I(i,j)$来表示像素值(RGB三通道分别处理), $\overrightarrow L(i, j)$来表示要流动的信息矢量, ${\overrightarrow{N}}(i,j)$来表示信息流动的方向, 总的更新公式为:  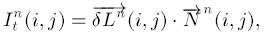 当流动达到收敛, $I^n(i, j)=I^{n+1}(i, j)$时, ${\overrightarrow{L}}(i,j)\cdot {\overrightarrow{N}}(i,j)=0$, 即二者相互垂直了. 因此, 不断重复上式的过程即可.
  这里有如下关系, 要流动的信息$L(i, j)$表示了像素的光滑程度, 也就是像素的二阶微分.
$L(i,j)=\frac{\partial I^2}{\partial x^2}+\frac{\partial I^2}{\partial y^2} = \frac{I(i,j+1)-2\ast I(i,j)+I(i,j-1)}{dx^2} + \frac{I(i+1, j)-2\ast I(i,j)+I(i-1,j)}{dy^2}$   信息矢量$\overrightarrow L(i, j)$有如下形式: 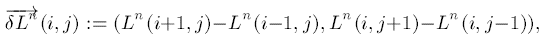  像素值的梯度方向: $\nabla I = (\frac{\partial I}{\partial y}, \frac{\partial I}{\partial y})$, 但inpainting需要的是梯度的法向方向: $\nabla^\top I = (-\frac{\partial I}{\partial x}, \frac{\partial I}{\partial y})$. 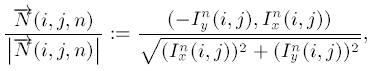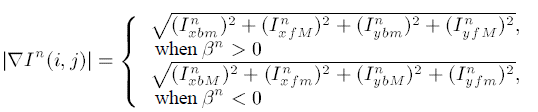所以, 信息流动单位矢量${\overrightarrow{N}}(i,j)$为   上面信息流动矢量是单位矢量, 还要乘上其模大小:  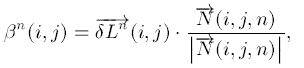 之所以要如此大费周章地化成单位矢量然后又乘以模, 是因为CFD中的数值不稳定性. 化成单位矢量的过程中求梯度的差分用的是中心差分, 乘以模的过程中求梯度的差分用的是前向(backward, 用b表示)和后向差分(forward, 用f表示), 否则程序容易发散. 详情参阅数值稳定性分析的内容, 那可是个大部头的书.
  上面的$\overrightarrow L(i, j)$和${\overrightarrow{N}}(i,j)$都确定后, 即可计算每次更新的$I_t$:
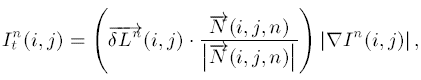  额外的, 文中还给出了关于像素$I$的扩散方程, 在经过上面的数次迭代过程后(对空缺区域补全), 对$I$进行少数的几次扩散(对边缘过渡区域进行羽化), 可以使结果更好.

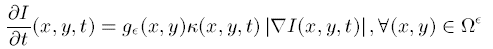
实验验证

  针对上图的测试案例, 采用Opencv的APIcv.inpaint得到结果如下:   自己用python的numpy复现了一下, 可以看到纹理的等值线在mask区域得到了延伸.
  针对自然场景, 用我们家的小肥猫做测试. mask确实不见了, 总体视觉效果可以, 但是也存在部分纹理失真, 比如脸上的八字出现了折线, 鼻头部分缺失等. 这里, 自己跑的结果看起来比OpenCV好的原因是经过了更长次数的迭代, 相比起来时间要长了很多.   代码如下(与原文不同的是这里没有求解$I$的扩散方程, 因为不清楚方程具体的离散方式):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
    for t in range(nt):
        old_edit = edit.copy()

        # step 1: 求解矢量L
        laplacian = np.zeros_like(edit)
        laplacian[1:-1, 1:-1] = 1 / dx**2 * (edit[1:-1, 2:] - 2 * edit[1:-1, 1:-1] + edit[1:-1, 0:-2]) + \
                                    1 / dy**2 * (edit[2:,1: -1] - 2 * edit[1:-1, 1:-1] + edit[0:-2, 1:-1])
            
        laplacian_delta_i = np.zeros_like(laplacian)
        laplacian_delta_j = np.zeros_like(laplacian)
        laplacian_delta_i[1:-1, :] = laplacian[2:, :] - laplacian[0:-2, :]
        laplacian_delta_j[:, 1:-1] = laplacian[:, 2:] - laplacian[:, 0:-2]
            
        # step 2: 求解I的梯度及矢量N
        edit_partial_i_central = np.zeros_like(edit)
        edit_partial_j_central = np.zeros_like(edit)
        edit_partial_i_central[1:-1, :] = (edit[2:, :] - edit[0:-2, :])/dy/2
        edit_partial_j_central[:, 1:-1] = (edit[:, 2:] - edit[:, 0:-2])/dx/2
        
        edit_partial_i_back = np.zeros_like(edit)
        edit_partial_j_back = np.zeros_like(edit)
        edit_partial_i_back[1:-1, :] = (edit[1:-1, :] - edit[0:-2, :])/dy
        edit_partial_j_back[:, 1:-1] = (edit[:, 1:-1] - edit[:, 0:-2])/dx
        
        edit_partial_i_forward = np.zeros_like(edit)
        edit_partial_j_forward = np.zeros_like(edit)
        edit_partial_i_forward[1:-1, :] = (edit[2:, :] - edit[1:-1, :])/dy
        edit_partial_j_forward[:, 1:-1] = (edit[:, 2:] - edit[:, 1:-1])/dx
        
        partial_norm = np.sqrt(edit_partial_i_central**2 + edit_partial_j_central**2)
        direct_i =  -edit_partial_j_central/(partial_norm + 1e-6)
        direct_j =  edit_partial_i_central/(partial_norm + 1e-6)
        
        # step 3: 求解两个矢量的点积
        beta = np.zeros_like(edit)
        beta = laplacian_delta_i*direct_i + laplacian_delta_j*direct_j
            
        # step 4: 求解模
        iterm1 = np.sqrt((np.minimum(edit_partial_j_back, 0))**2 +\
                    (np.maximum(edit_partial_j_forward, 0))**2 +\
                    (np.minimum(edit_partial_i_back, 0))**2 +\
                    (np.maximum(edit_partial_i_forward, 0))**2)
        iterm2 = np.sqrt((np.maximum(edit_partial_j_back, 0))**2 +\
                        (np.minimum(edit_partial_j_forward, 0))**2 +\
                        (np.maximum(edit_partial_i_back, 0))**2 +\
                        (np.minimum(edit_partial_i_forward, 0))**2)
        norm_image = np.where(beta>0, iterm1, iterm2)
        
        # step 5: 得到更新值dI
        delta_image = beta*norm_image
        
        # step 6: 更新I
        edit = edit + dt*delta_image
        
        # step 7: 施加边界条件
        edit = np.where(mask_crop==0, origin_crop, edit)

论文链接: Image Inpainting

  • Navier-Stokes, Fluid Dynamics, and Image and Video Inpainting (year 2001, cite 1050)

  这篇文章是在上篇文章的基础上做延伸, 都是用CFD的方法让像素流动. 但这里求解的不再是关于像素$I$的方程, 而是求解像素$I$的二阶微分的对流扩散方程.

理论推导

  针对不可压缩无旋流动, 有著名的Navier-Stokes方程: 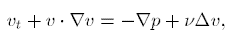  对上式两边同时作用算子$\nabla \times$, 得到关于涡量$\omega$的输运方程: 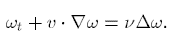  而上式在到达稳态后, 第一项和第三项消除, 有如下形式: 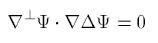  上式与上一篇文章中的${\overrightarrow{L}}(i,j)\cdot {\overrightarrow{N}}(i,j)=0$本质上相同的. 所以作者认为可通过求解涡量$\omega$的输运方程来达到同样的目的, 对此针对各个物理量同图像算法中的量做了类比:   额外的, 在经过几次对流扩散求解后(补全mask区域), 还要求解$I$的泊松方程(对过渡区域进行羽化): 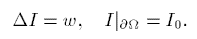  文中采用的是假设时间项的超松弛迭代法:

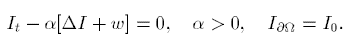
实验验证

  代码如下(只求解了$I$的泊松方程, 并没有求解$\omega$的输运方程):

1
2
3
4
5
6
7
8
9
10
11
12
13
    dx = 1
    dy = 1
    dt = 0.001
    alpha = 2
    nstep = 3000
    
    for step in range(nstep):
        # 求解I的泊松方程
        edit[1:-1, 1:-1] += dt*alpha*(1 / dx**2 * (edit[1:-1, 2:] - 2 * edit[1:-1, 1:-1] + edit[1:-1, 0:-2]) +
                        1 / dy**2 * (edit[2:,1: -1] - 2 * edit[1:-1, 1:-1] + edit[0:-2, 1:-1]))
        
        # 施加边界条件
        edit = np.where(mask_crop==0, origin_crop, edit)

论文链接: Navier-Stokes, Fluid Dynamics, and Image and Video Inpainting

评价与思考

  借鉴了流体力学的思想, 让像素像流体般流动, 且流动是按照纹理的方向来运动, 这种idea是很好的. 但是在实际操作的过程中, 也发现了一些存在的问题. 一, CFD方法需要迭代求解, 速度很慢; 二, CFD对网格以及离散格式要求很高, 稍不留心就容易发散; 三, 只适用于小块儿的mask, 对于大块儿的mask由于缺失信息过多, 要想补全的话, 还是得依靠深度学习的方法, 从大数据中取得缺失信息的先验.


「评论区」：